Mein BB (Inflation)

Nachdem wir die grundsätzliche Berechnung des Schallhorizontes DS=dS/a geklärt haben, gilt es noch, die Diskrepanz zum ersten Peak zu klären.
r* = DS = 144,43 Mpc = 471 Mly (CODATA)
dS = DS·a = 432 kly = 132,4 kpc
θ* = r*/dC = 0,0104092 = 0,5964° (CODATA) acoustic scale

Der erste Peak befindet sich beim Multipol li=220,6 und somit bei θi=π/li=0,01424=0,816°=48,96'. Dieser Radius beträgt somit
ri = θi·dA = 591 kly = 181 kpc
bzw mitbewegt θi·dC = ri/a = 644 Mly = 198 Mpc

Es ist natürlich so, dass eine Kontraktion nicht davon abhängt, dass die Druckwelle von ganz außen nach ganz innen gelangt. Vielmehr kontrahiert ja die gesamte Region. Allerdings basiert der Peak darauf, dass die Oszillation gerade zum Stillstand gekommen ist, weil der Strahlungsdruck die Kontraktion aufgehalten hat. In dieser zeitlichen Situation ist die Bewegung der Dichtefluktuation am langsamsten und daher wird die Häufung vieler ähnlicher Kontraktionen als Peak sichtbar.

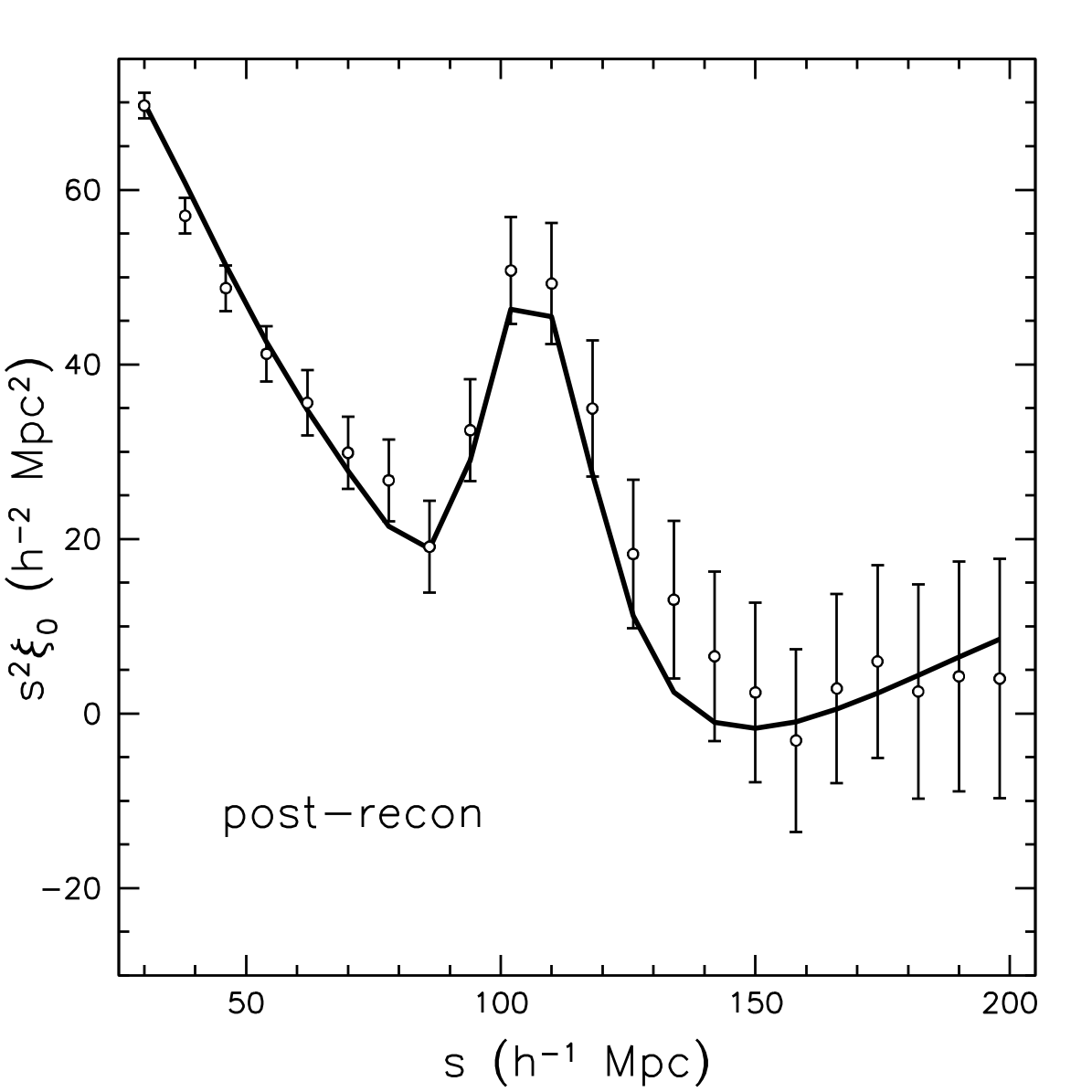
In diesem Zusammenhang ist auch interessant, dass BOSS des SDSS diesen Peak bestätigt hat bei ca
r = 100/h Mpc = 148 Mpc = 484 Mly
bzw bis zu 115/h Mpc = 171 Mpc = 556 Mly

Damit wurde sowohl die Flachheit des Universums belegt, als auch die Korrektheit der Rückschlüsse aus der CMB.

Allerdings liegt dieser Bereich nun zwischen dem Schallhorizont und dem ersten Peak....ganz exakt stimmt alles nicht gerade überein.

Rainer Raisch schrieb:

cS = ²(d.p/d.ρ) = ²(p/ρ) = c/²3

Hier explizit:
www-zeuthen.desy.de/~kolanosk/astro0506/skripte/kosmos03.pdf
(2.81)

Die Daten sind zwar veraltet (WMAP vor Planck)

Irgendwo hatte ich einen Thread eröffnet, um die richtige Verdünnung der Materie zu berechnen, denn üblich läst man die Kinetische Energie einfach unter den Tisch fallen. ich kann das aber nicht finden.

Die Verlangsamung der Pekuliargeschwindigkeit und damit die Verdünnung der Kinetischen Energie folgt dem skalierten relativistischen impuls.

a·β·c·γ = a'·β'·c·γ'

Nun ist mir klar geworden, dass ich ja die Entwicklung von γ'/γ suche, die Geschwindigkeit selbst ist ja in diesem Zusammenhang uninteressant.
γ'/γ = a·β/a'β'

Aus der Formel kann man aber auch β' ersetzen, ohne erneut γ und γ' einzuführen, weil sich ja die Lorentzfaktoren γ und γ' entsprechend durch β und β' ersetzen lassen:
β' = a·β/²(a²β²-a'²β²+a'²)

Dies kann man in die obere Formel einsetzen und erhält
γ'/γ = ²(a²β²-a'²β²+a'²)/a' = ²(a²β²/a'²-β²+1)

Somit verdünnt bewegte Materie mit der Expansion mit dem Faktor:
²(β²/a²-β²+1)/a³ EDIT: wer hatte da den Bruchstrich geklaut....
mit β Anfangsgeschwindigkeit und a = a₂/a₁

Habe ich einen Dreher oder sonstigen Fehler drin?

Wie man sieht, ergibt sich aus β=1 → 1/a⁴ wie für Strahlung und für β=0 → 1/a³ wie es für Materie die übliche Formel ist.

Das hatten wir damals im alten Forum im Zusammenhang mit dem Thema wie schnell die Neutrinos heute wären wenn sie bei der Emission soundso schnell gewesen wären, irgendwo ist das sogar noch archiviert aber frage nicht wo. Der Impuls p=mvγ oder p=h/λ ist jedenfalls invers proportional zum Skalenfaktor a, E²=m²c⁴+p²c² und ρ ist proportional zu E/a³.

So lang ist das schon her... ich hatte das mehrmals thematisiert und dachte die letzte Rechnung müsste hier gewesen sein. Egal, endlich habe ich die Formel.

Rainer Raisch schrieb:

Somit verdünnt bewegte Materie mit der Expansion mit dem Faktor:
²(β²/a²-β²+1)/a³
mit β Anfangsgeschwindigkeit und a = a₂/a₁

Das kann man auch umformen, wem es besser gefällt:
²(β²/a²-β²+1)/a³ = ²(β²-β²a²+a²)/a⁴ = ²((a-β)²+a²β²)/a⁴ = ²(1-β²(1-1/a²))/a³

Mit a₂=1 und a=a₁ ergibt sich der Faktor 
²(β²a²-β²+1)a³ = a^(ln.(²(1+²(a²-1)β²)a³)/ln.a) = a³+a^(ln.(²(1+²(a²-1)β²)a³-a³)/ln.a)


Somit lässt sich die Kinetische Energiedichte θ als eigenständige Komponente separieren, allerdings für jede Anfangsgeschwindigkeit anders.
θ ~ 1/a^(ln.(²(1+²(a²-1)β²)a³-a³)/ln.a)

Rainer Raisch schrieb:

Ich habe das Video gefunden ab Std 1 Min 50

In diesem Video spricht Susskind über die Baryogenese (Antimateriedefizit).

Wenn die Expansion (Inflation) sehr schnell ist, gibt es keine Zeitsymmetrie (T), weshalb auch die CP-Symmetrie nicht mehr gewährleistet ist.
Dies liegt daran, weil die Quantenvorgänge keine ausreichende Zeit haben, bevor sie durch die Expansion gestört werden.
Ist zB die Reichweite eines virtuellen Teilchens größer als der Hubble Radius, dann kann die QF zerrissen werden.
Die übliche Herangehensweise ist, die Zerfallsbreite oder allgemein Halbwertbreite ΓZ mit dem Hubbleparameter H zu vergleichen.

ΓZ/ℏ = 1/τZ = ln.2/τ½ = λZ = n·v·σA
mit Wirkungsquerschnitt σA, Lebensdauer τZ, Halbwertzeit τ½ und Reaktionsrate λZ

Wie wir gesehen haben, wird die Hawkingstrahlung ernsthaft für das expandierende Universum unterstellt.

Rainer Raisch schrieb:

Hier eine Übersicht (Kaustuv Basu WS 22/23)
astro.uni-bonn.de/~kbasu/CMB/Online_Slid...0Polarization-II.pdf
Why inflation would produce GW?
Er begründet es mit einer Analogie der bzw mit der Hawkingstrahlung.

Wie wäre es nun, wenn die Hawkingstrahlung Materie der Antimaterie vorzieht, also die CP-Symmetrie verletzt? Bei der Hawkingstrahlung werden ja einzelne Teilchen erzeugt und keine Paarbildung. Die Verletzung ist naturgemäß immer klein, daher entsteht das Gros zu gleichen Teilen, aber es kann eine Asymmetrie entstehen, also der Materieüberschuss. Womöglich kann man dies sogar statistisch begründen.

Nun nochmals zu meinem Modell des Beginns der Inflation:
H = 0 Anfangswert
K = 1/rP² anfängliche sphärische Krümmung

In meinem Modell gibt es ja zuerst nur falsches Vakuum mit hoher Energiedichte. Bei der Entstehung ist die Hubblerate zwar zuerst H=0 1/s, bei maximaler Krümmung R=1/rP, das falsche Vakuum beschleunigt allerdings rasant.

FrI = H² = c²Λ/3-c²K = 0
Λ = 3/rP² Anfangswert falsches Vakuum
FrII = ä/a = c²Λ/3 = 1/tP² Anfangswert

Am Hubble Radius herrscht dann immer die kinematische Beschleunigung
κ = H·c = H²rH
und somit die Hawkingstrahlung oder sagen wir lieber Unruhstrahlung (rechnerisch identisch) mit der Temperatur
TU = κ·kU = H·c·kU = ℏH/(2π·kB) = c₂H/(2π)²c = c₂/4π²rH
mit einer Luminosität (Leistung)
L = TU²kB²π/240ℏ = H²ℏ/960π
und somit eine Dichteänderung (Leistungsdichte) von 
IE = c²d.ρ/d.t = L/V = H²ℏ/1280π²rH³ = H⁵ℏ/1280π²c³
Nach der Flussgleichung von Friedmann verdünnt sich die Strahlungsdichte mit
Frρ = -3H(c²ρr+pr) = -4H·c²ρr
Es stellt sich die Frage, wann beides "gleich groß" ist, so dass das Slow Rolling stattfindet:
0 = IE+Frρ
4H·c²ρr = H⁵ℏ/1280π²c³
c²ρr = H⁴ℏ/5120π²c³

In meinem Modell entwickelt sich H, allerdings ohne Strahlung, wie
H(τ) = tanh.(τ/tP)/tP
Zudem sollte durch die entstehende Strahung auch die Vakuumenergiedichte sinken, denn von irgendwo muss die Energie ja kommen, wie beim SL.
H verhält sich zur Gesamtenergie (ρ = ρλ+ρr)
ρλ = ρ-ρr
H² =  8πG·ρ/3

EDIT:
Am Anfang darf man die Krümmung nicht vernachlässigen.
ρk(a) = 3/(8π·tP²a²G)

wie geht es weiter?

Rainer Raisch schrieb:

EDIT:
Am Anfang darf man die Krümmung nicht vernachlässigen.

Dies hat ua zwei wichtige Konsequenzen:
1) Das Volumen berechnet sich nicht als Kugel sondern als Polkappe (Kalotte)
V = 2R³π² Gesamtvolumen
VH = R³π(2rH/R-sin.(2rH/R)) Hubblevolumen (rH < r)
SH = 4R²π(sin.(rH/R))² Hubblesphäre (Kalottenmantel)
2) Solange der Hubbleradius größer als r ist, gibt es gar keinen Ereignishorizont und somit keine Hawkingstrahlung.

0) Aus dem Anfangswert
H₀ = 0
ergibt sich der anfängliche Hubbleradius
rH₀ = c/H₀ → ∞

1) Mit der Beschleunigung vergrößert sich der Wert von H und das Universum expandiert beschleunigt. Nehmen wir für diese erste Phase den Index ₁. r₁ vergrößert sich und rH₁ verkleinert sich in dieser Phase mit der Expansion.
H₁ = tanh.(τ/tP)/tP
rH₁ = rP/tanh.(τ/tP)
a₁ = a₀·cosh.(τ/tP)
R₁ = R₀·a₁/a₀ = R₀·cosh.(τ/tP)
Λ₁ = Λ₀ konstant

r) Um den Moment (Index ᵣ) zu berechnen, wenn der Hubbleradius innerhalb des Universums liegt, also wirksam wird, setzen wir
rᵣ = rH₁ = r₁ = π·R₁
und wir erhalten
rP/tanh.(τ/tP) = π·R₀·cosh.(τ/tP)
rP = π·rP·sinh.(τ/tP)
τᵣ = asinh.(1/π)tP = 0.313 tP
aᵣ/a₀ = a₁/a₀ = cosh.(τᵣ/tP) = cosh.(asinh.(1/π)) = ²(1/π²+1) = 1,0494385 EDIT Rechenfehler
rᵣ = π·Rᵣ = π·R₀·aᵣ/a₀ = 1,0494385π·rP = 3,2969 rP
Vᵣ = 2Rᵣ³π² = 2rᵣ³/π = ²(1/π²+1)³2π²rP³ = 22,81396 rP³

2) In diesem Moment beginnt die Hawkingstrahlung und die zweite Phase (Index ₂) beginnt
Hᵣ = tanh.(τᵣ/tP)/tP = tanh.(asinh.(1/π))/tP = 1/²(π²+1)tP = 0,30331 1/tP EDIT: Bruchstrich fehlte
TH₂ = H₂·c·kU
THᵣ = 6.83935998e+30 K einsetzende Hawkingstrahlung,
Lᵣ = THᵣ²kB²π/240ℏ = 1.1e+48 W
Lᵣ/Vᵣ = 4,8216e+46 W/rP³
wodurch falsche Vakuumenergie in reelle Strahlung verwandelt wird und was den Wert von Λ₀ senkt und den Wert der Strahlungsdichte ρr steigert, welche wiederum durch die Expansion mit 1/a⁴ gesenkt wird.

Rainer Raisch schrieb:

SH = 4R²π(sin.(rH/R))² Hubblesphäre (Kalottenmantel)

Dies erscheint nicht ganz korrekt.
Wir müssen hier noch eine weitere Phase einschieben, und zwar für rH > r/2, weil die Breitenkugeln (vergleichsweise die Breitenkreise) südlich des Äquators wieder kleiner werden, bzw in Gegenrichtung betrachtet, erst langsam größer werden, bis beim Äquator das Maximum der Großkugel (vgl Großkreis) erreicht wird und dann die Breitenkreise wieder kleiner werden.

i) Phase 1: r < rH
ii) Phase 2: r/2 < rH < r = π·R
iii) Phase 3: rH < r/2 = π·R/2

zum Glück erledigt dies die Sinusfunktion automatisch
SHi = 0
SHii = 4R²π(sin.(rH/R))²
SHiii = 4R²π(sin.(rH/R))² Hubblesphäre (Kalottenmantel)

Beim Volumen erledigt sich dieses Problem ebenfalls durch die Sinusfunktion
VHi = 0
VHii = R³π(2rH/R-sin.(2rH/R))
VHiii = R³π(2rH/R-sin.(2rH/R)) Hubblevolumen

Rainer Raisch schrieb:

mit einer Luminosität (Leistung)
L = TU²kB²π/240ℏ = H²ℏ/960π

Das Problem ergibt sich für die Luminosität, die natürlich von dieser Horizontfläche abhängt, meine Formel galt lediglich für die flache Geometrie,
Lσ = L/S Radianz
L' = Lσ·S' korrigierte Luminosität
Korrekturfaktor somit SH/SK (Kalottenhorizont/Kugeloberfläche)
LHi = 0
LHii = TU²kB²π/240ℏ·(SHii/SK)
LHiii = TU²kB²π/240ℏ·(SHiii/SK)
mit SK = 4rH²π Kugeloberfläche
SHii/SK = SHiii/SK = 4R²π(sin.(rH/R))²/4rH²π = (sin.(rH/R)R/rH)² → 1 für R → ∞

Somit beginnt die Hawkingstrahlung also bei τr erst ganz sachte und nicht abrupt. Erst für rH < r/2 ergibt sich die Wirkung der vollen Hubblesphäre, wobei aber ebenfalls die Krümmung zu Buche schlägt. Da die Formeln ii und iii für diese beiden Phasen 2 und 3 gleich sind, könnte man sie doch wieder zusammenfassen, ich denke aber, das sollte man zur Veranschaulichung trotzdem getrennt betrachten.

Hier beschreibt Susskind die Nullpunktfluktuationen des Inflatonfeldes als gedämpften Oszillator.

Das Slow Rolling wird als unterdämpfte Oszillation beschrieben.
Der Kipppunkt ist die kritische Dämpfung, bei der die Nullpunktfluktuation infolge der inflationären Expansion die Wellenlänge des Hubble Radius erreicht. Genau genommen spricht Susskind von r = λ/2π = 2/3 rH. Danach verläuft die Oszillation überdämpft, was bedeutet, dass sie einfriert und von der Expansion räumlich vergrößert und ausgedünnt wird. Da beständig neue Fluktuationen erzeugt werden, ergibt sich eine Überlagerung aller möglicher Größen und Dichten.

Sobald das Inflatonfeld "über die Klippe rollt", (bzw auch erst nahe der Talsohle) verwandelt es seine Nullpunktenergie in reelle Teilchen. Die während des Slow Rolling generierten Dichteschwankungen ergeben dabei reelle Dichtefluktuationen, wie sie später in der CMB sichtbar werden.
EDIT: In einer vorherigen Lektion präzisiert Susskind dies dahin, dass es dabei nur um die größten Strukturen (Filamente) geht.

Mit anderen Worten, und Susskind sagt das an einer Stelle ausdrücklich, handelt es sich ausschließlich um die Fluktuationen des Inflatonfeldes, die die Dichtefluktuationen erzeugen. Damit kann man auch sagen, dass Λ immer konstant ist, jedoch in dieser Phase mit dem Inflatonfeld als zusätzliche Komponente zu rechnen ist. Nach diesem Modell ist da gar nichts mit Hawkingstrahlung, sondern ausschließlich das Inflatonfeld ist für die heutige reelle Energie verantwortlich.

ab Min 37:

Gute Erklärung der diversen Horizonte in der Kosmologie von Harald

Mit der Inflation hat dies zwar gar nichts zu tun:

Ich hatte in einigen Artikeln gelesen, dass das Universum ein BEC (Bose-Einstein-Kondensat) war, dies soll mit z=8150000 also erst ca 32 Tage nach dem Urknall geendet haben (T = z·T° = 1900 eV/kB)

Leider kann ich dazu gar nichts mehr finden und wollte dies nun selber berechnen. Dabei ist eigentlich klar, dass es vor der Higgsära (Thig = 159,5 GeV/kB) keine Elementarteilchen mit Masse gab, also ein BEC illusorisch ist. Nachdem das confinement wirksam wurde, war die Temperatur (Thag = 156,5 MeV/kB) allerdings zu gering für schwerere Teilchen, im thermodynamischen Gleichgewicht zu bleiben. Es kämen daher wohl gar keine neue geeignete Teilchen mehr in Betracht, sondern nur in der Zwischenzeit und nur (Bosonen!) W (80,377 GeV/kB) und Z ( 91,1876 GeV/kB). Aber egal ....

Ein BEC entsteht, wenn, bzw erfordert, dass die de Broglie Wellenlänge größer ist als der Teilchenabstand
λB > λØ
weil sich dann die Teilchen überlappen und nur dann im selben Quantenzustand existieren können, wenn sie ein derartiges Kondensat bilden. Die Berechnung für das thermodynamische Gleichgewicht ergibt nun zur Überraschung, dass immer gilt
λB/λØ = 2,82971 für Fermionen bzw
λB/λØ = ³(4/3)λB/λØ = 3,1144997 für Bosonen, wie es ja beim BEC sein muss
und zwar unabhängig von Masse oder Temperatur, solange es eben ein thermodynamisches Gleichgewicht (inkl Paarbildung) der Teilchen mit der bb-Strahlung ist.

Die Unabhängigkeit von der Masse könnte bedeuten, dass auch vor der Higgsära ein BEC herrschte, als alle Elementarteilchen in der Form von masseloser Strahlung vorlagen. Jedoch setzt dies wohl eine Übereinstimmung der Frequenz voraus, was gerade nicht vorliegt.
KI:
Ein Photonen-Bose-Einstein-Kondensat (auch „Super-Photon“ genannt) ist ein makroskopischer Zustand des Lichts, in dem sich eine große Anzahl von Photonen kollektiv so verhält, als wären sie ein einziges, riesiges Teilchen. Dies geschieht, indem Photonen in einem optischen Resonator – einem Behälter mit einem Farbstoff – eingefangen und zu einem gemeinsamen Quantenzustand gezwungen werden, wodurch sie Eigenschaften eines Bose-Einstein-Kondensats annehmen. Dieses Phänomen wurde erstmals 2010 erzeugt und kann zu neuen Lichtquellen mit laserähnlichen Eigenschaften führen

Allerdings kann ich mir keine Teilchen (Bosonen!) vorstellen, die zu späten Zeiten ein BEC gebildet hätten, elementare Bosonen gibt es ja sonst nicht und zusammengesetzte (zB Helium) wären zu kalt und zu dünn. Den Grenzfall λB/λØ=1 habe ich jetzt zwar nicht berechnet. Bei der geringen Dichte von Helium in der BBN erübrigt sich dies jedoch sowieso.

Welche Randbedingung jedoch zur Zeit z=8150000 eingetreten sein soll, kann ich nicht erkennen.

Rainer Raisch schrieb:

a·β·c·γ = a'·β'·c·γ'

Ich habe das nochmal ausgerechnet, wie sich die Geschwindigkeit entwickelt (mit ϙ=a'/a) und (u und u' sind durch c dividiert)
1/γ² = 1-u²
u' = u/²(u²+ϙ²/γ²)

Hier die Diagramme für Werte von u=0,1 bis u=0,99
neben a' > a ist auch a > a' berechnet, die lila Kurve für u=0,5 beginnt zB bei u'/u=2, somit wird c nie überschritten.

Rainer Raisch schrieb:

a·β·c·γ = a'·β'·c·γ'
γ'/γ = ²(a²β²-a'²β²+a'²)/a' = ²(a²β²/a'²-β²+1)

Somit verdünnt bewegte Materie mit der Expansion mit dem Faktor:
²(β²/a²-β²+1)/a³
 

und hier der Vergleich des Energieverlustes (γ'/γ) von Materie gegenüber (unterste rote Kurve) Licht (f'/f=a/a'):

Und hier noch der Vergleich allein der Kinetischen Energie (T'/T) mit der obersten roten Kurve für Licht (f'/f=a/a')

T'/T = (γ'-1)/(γ-1) = (1-sqrt(1-1/(1+(u²-1)(Kop.a)²)))/sqrt(1-1/(1+(u²-1)(Kop.a)²))/(-1+1/sqrt(1-u²))



Und hier noch der unmittelbare Vergleich mit Licht = 1
T'/f'

Rainer Raisch schrieb:

Jedoch setzt dies wohl eine Übereinstimmung der Frequenz voraus, was gerade nicht vorliegt.

naja es gibt immer ein Schwerpunktsystem mit identischen Frequenzen der beiden Teilchen. Da beide Teilchen masselos sind, ist die Frequenz sogar vollkommen egal. Soweit ich es sehe, werden alle Teilchensorten dann zufäiig und somit mit gleicher Dichte erzeugt (bei höherer Dichte steigt die Umkehrreaktion der Annihilation). Genau so ist das thermodynamische Gleichgewicht definiert. Die Masse der Teilchen ist dabei irrelevant (solange Paarerzeugung möglich ist). Naja die Freiheitsgrade können unterschiedlich sein, daher gibt es mehr Quarks mit 3 unterschiedlichen Farbladungen und weniger Neutrinos da es (vermutliche) Majoranateilchen (Nspin·Nparity = 2), wie beim Photon, sind

Rainer Raisch schrieb:

Außerdem sind ja vorher alle Elementarteilchen masselos, nebst den zugehörigen Antiteilchen. Ich bin mir zwar nicht sicher, welche Auswirkung dies auf den Freiheitsgrad ihres Spins hat.

Ich habs.
Für die meisten Elementarteilchen ändert sich dadurch nichts, sie haben vor der Higgsära genau gleich viele Freiheitsgrade wie nachher.

Es gibt jedoch einen Unterschied bei Bosonen Z und W:

Diese haben als massebehaftete Bosonen mit dem Spin 1 drei Spinzustände (-1, 0, +1)
In der masselosen Zeit haben sie jedoch nur 2 Spinzustände (-1, +1) da sie bei v=c nicht mehr in der Bewegungsrichtung oszillieren können.

Somit ergeben sich vor der Higgsära 2(Photonen)+1(H)+2·1(Z)+2·2(W)+2·8(Gluonen)+6·2·2·3(Quarks)+3·2·1(Neutrinos)+3·2·2(e+μ+τ) Freiheitsgrade. Allerdings treten die Fermionen nur mit einem Faktor 7/8 gegenüber Bosonen auf.
2+1+2·1+2·2+2·8+(6·2·2·3+3·2·1+3·2·2)7/8 = 103.75

Nach der Higgsära verschwinden allerdings die Teilchen, die mehr Energie benötigen als noch vorhanden ist (T = 1,851e+15 K = 159,5 GeV/kB. Das top Quark (172,69 GeV) friert daher aus. Stattdessen werden W und Z mit nunmehr 3 Freiheitsgraden aufgefüllt.
2+1+3·1+2·3+2·8+(5·2·2·3+3·2·1+3·2·2)7/8 = 96,25

Als nächstes frieren Higgs (125 GeV) danach Z (91,2 GeV) und W (80,4 GeV) aus, dann bottom Quark (4,18 GeV), Tauon (1,777 GeV) und charm Quark (1,27 GeV), bis die Hagedorn Ära (156,5 MeV) beginnt.
2+3·1+2·3+2·8+(5·2·2·3+3·2·1+3·2·2)7/8 = 95,25
2+2·3+2·8+(5·2·2·3+3·2·1+3·2·2)7/8 = 92,25
2+2·8+(5·2·2·3+3·2·1+3·2·2)7/8 = 86.25
2+2·8+(4·2·2·3+3·2·1+3·2·2)7/8 = 75,75
2+2·8+(4·2·2·3+3·2·1+2·2·2)7/8 = 72,25
2+2·8+(3·2·2·3+3·2·1+2·2·2)7/8 = 61,75

Mit der Hagedorn Ära (156,5 MeV) entsteht das Confinement, die Quarks sowie Gluonen verschwinden daher und sind nur noch in gebundener Form vorhanden. Soweit ich sehe, kommen dafür nur Pionen (134-139 MeV) in Frage. Pionen sind zwar Bosonen haben aber nur einen Spin (0) kommen jedoch in 3 Ladungsvarianten (-1, 0, +1) vor. Proton (938 MeV) und Neutron (939 MeV) frieren jedoch wegen der hohen benötigen Energie sofort aus.
2+(3·2·1+2·2·2)7/8+3 = 17,25

Sodann verschwindet das Pion (134-139 MeV). Sodann verschwindet auch das Myon (105,7 MeV)
2+(3·2·1+2·2·2)7/8 = 14,25
2+(3·2·1+1·2·2)7/8 = 10,75

Die Neutrinos frieren aus, sobald ihr Wirkungsquerschnitt zu klein wird, bei T=0,8444 MeV/kB allerdings annihilieren sie nicht, sondern nehmen nur ab sofort nicht mehr am thermodynamischen Gleichgewicht teil.
2+(2·2)7/8 = 5,5

Zuletzt frieren die Elektronen (511 keV) aus und es bleiben nur noch Photonen im thermodynamischen Gleichgewicht mit sich selbst
2

Die Freiheitsgrade können dabei (in der strahlungsdomierten Phase) unmittelbar als Faktor zwischen Temperatur und Dichte eingesetzt werden, wobei  das Photon (Faktor 2) üblich in den Formeln bereits berücksichtigt wurde. Lediglich die Neutrinos sind gesondert zu bewerten

ρ = Nf·T⁴σₐ/2c² + ρny
Die Gesamtdichte steht wieder mit H=²(ρ/ρ°)H°=²(ρ·8π·G/3) in direktem Zusammenhang.
 

Rainer Raisch schrieb:

Die Neutrinos frieren aus, sobald ihr Wirkungsquerschnitt zu klein wird, bei T=0,8444 MeV/kB allerdings annihilieren sie nicht, sondern nehmen nur ab sofort nicht mehr am thermodynamischen Gleichgewicht teil.
2+(2·2)7/8 = 5,5

Zuletzt frieren die Elektronen (511 keV) aus und es bleiben nur noch Photonen im thermodynamischen Gleichgewicht mit sich selbst
2

Da rechnet man die Neutrinos nicht getrennt, sondern mit der um den Faktor ³(4/11) reduzierten Temperatur, sobald die Photonen im Gegensatz zu den ausgefrorenen Neutrinos durch die Annihilation der Elektronen dementsprechend aufgeheizt werden. Daher ändert sich an der Anzahl der Freiheitsgrade erstmal nichts, bis die Elektronen ausfrieren. Dennoch erscheint es mir sachgerechnet, die beiden Anteile gesondert zu notieren, denn die Neutrinos sind nicht im thermodynamischen Gleichgewicht mit den Photonen, sie entwickeln sich nur analog.
2+(2·2)7/8+(3·2)7/8 = 10,75 = 5,5+5,25
2+(3·2)7/8·³(4/11)⁴ = 3,3626439 = 2+1,3626439

Die Konsequenz dieser reduzierten Freiheitsgrade nf (üblich g*) ist ja eine Verringerung der Dichte.
ρ = ρ.gam·nf/2

Während der Annihilation wird jedoch die Temperatur erhöht bzw konstant gehalten. Allerdings ist mir aufgefallen, dass es ja nicht genügt, nur die Temperatur auf die geringeren Freiheitsgrade zu verteilen, sondern die Masse wird bei der Annihilation ebenfalls in Energie verwandelt. Bei c²m=T·kB ist dies immerhin ein Beitrag in gleicher Höhe γ=2. 

Da muss ich meine ganzen weiteren Rechnungen erst noch überdenken.

Rainer Raisch schrieb:

Allerdings ist mir aufgefallen, dass es ja nicht genügt, nur die Temperatur auf die geringeren Freiheitsgrade zu verteilen, sondern die Masse wird bei der Annihilation ebenfalls in Energie verwandelt. Bei c²m = T/kB ist dies immerhin ein Beitrag in gleicher Höhe γ=2. 

Das war Unsinn. Bei T·kB = c²m (abgesehen von meinem Dreher) geht man davon aus, dass das Elementarteilchen gar keine Kinetische Energie mehr abbekommt oder mitbringt.