klassisch kontra relativistisch

Variante 1) Klassisch:
Auf einer 9-spurigen Autobahn befinden sich 9 Autos (Auto 1 – 9)
Jedes Auto hat seine eigene Uhr im Auto. Nun fahren alle Autos nach ihrer eigenen Uhr 1 Stunde lang nach vorne,
dann bleiben sie stehen (Beschleunigung und Verzögerung vernachlässigt) Ob sie genau gleichzeitig fahren oder nicht, ist bedeutungslos.
Auto 1 fährt mit 111 km/h 
Auto 2 fährt mit 222 km/h 
Auto 3 fährt mit 333 km/h
Auto 4 fährt mit 444 km/h
Auto 5 fährt mit 555 km/h
Auto 6 fährt mit 666 km/h
Auto 7 fährt mit 777 km/h
Auto 8 fährt mit 888 km/h
Auto 9 fährt mit 999 km/h
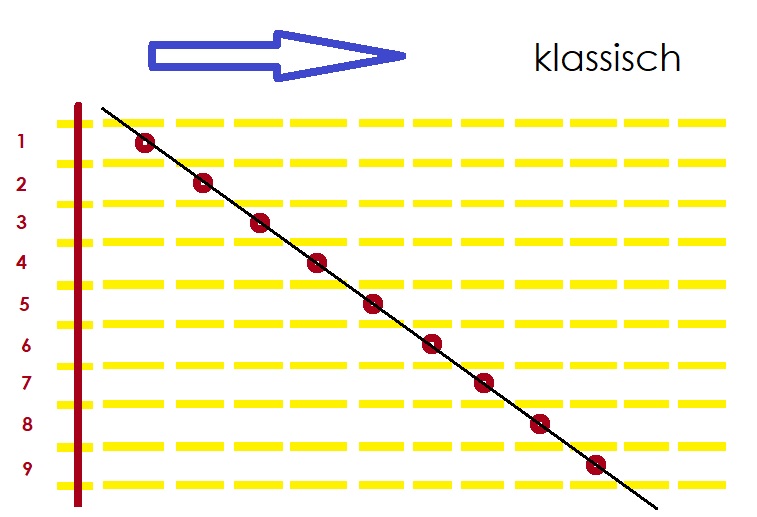
Nachdem alle stehen, kann man eine gerade Linie durch alle Autos ziehen. Das ist unbestritten.




Variante 2) Relativistisch:
Alle Autos fahren 1 Sekunde lang nach ihrer eigenen Uhr und bleiben dann stehen.
Auto 1 fährt mit 0,111 c 
Auto 2 fährt mit 0,222 c
Auto 3 fährt mit 0,333 c
Auto 4 fährt mit 0,444 c
Auto 5 fährt mit 0,555 c
Auto 6 fährt mit 0,666 c
Auto 7 fährt mit 0,777 c
Auto 8 fährt mit 0,888 c
Auto 9 fährt mit 0,999 c
Nachdem alle Autos stehen, zieht man eine Linie durch alle Autos
Wird die Linie gerade? oder nach oben gekrümmt? oder nach unten gekrümmt?


Nachdem hier fast alle (außer mir) mit Zeitdilatation und Längenkontraktion rechnen können,
kann man ganz genau errechnen, wieweit jedes Auto fährt und ich werde dann die Grafik mit der Kurve machen.
Und dann schauen wir uns das genauer an.

 

badhofer schrieb:

Wird die Linie gerade? oder nach oben gekrümmt? oder nach unten gekrümmt?

Die Linie wird genauso gerade, an der Fragestellung ist nichts relativistisch. Sogar die vom Straßenrand aus beobachtete Geschwindigkeit und die am Tacho der Autos stimmt überein.

Das Problem dabei entsteht nur, wenn die Fahrer nach der eigenen Uhr 1 Sekunde lang fahren, dann ergeben sich natürlich schon Unterschiede, solange sie sich aber an der Stadionuhr orientieren, spielt es keine Rolle.

Wenn sie nach der eigenen Uhr 1 Sekunde fahren, dann sieht es vom Straßenrand beobachtet so aus, als ob sie schummeln und zu lange fahren, also auch eine jeweils noch größere Strecke, je scheller sie unterwegs sind.

Also in diesem interessanteren Fall ergibt sich folgende Strecke
s(β) = γβct
rechnen wir am besten in Einheiten von c·t=1 ls ≈ 300000 km Lichtsekunden
β=0,111 → s =  0.11169 ls
β=0,222 → s = 0.22768 ls
β=0,333 → s = 0.353 ls
β=0,444 → s = 0.4955 ls
β=0,555 → s = 0.667 ls
β=0,666 → s = 0.8928 ls
β=0,777 → s = 1.2343 ls
β=0,888 → s = 1.931 ls
β=0,999 → s = 22.3439 ls

Natürlich richtet sich jedes Auto an seiner eigenen Uhr. Anders wäre das in der Praxis gar nicht möglich.
Kannst du noch errechnen, wie viele Meter jedes einzelne Auto fährt?
Ich mache dann eine Grafik dazu. Aufgrund dieser Grafik ergibt sich eine weitere Frage.
 

Du willst Meter? Hier!

0.111 33'507'060
0.222 68'304'423
0.333 105'946'715
0.444 148'656'270
0.555 200'156'195
0.666 267'845'745
0.777 370'293'534
0.888 579'327'593
0.999 6'703'171'731

badhofer schrieb:

Nachdem hier fast alle (außer mir) mit Zeitdilatation und Längenkontraktion rechnen können

 

Woran liegt es denn, dass du es nicht kannst, badhofer? Beschäftigst dich ja schon eine Weile damit.
Das bisschen Mathematik kann man lernen. Nur etwas Bruchrechnen, Quadratwurzel ziehen/quadrieren, Gleichungen umformen.

Kannst du noch errechnen, wie viele Meter jedes einzelne Auto fährt?

Das wirst doch noch selber hinbekommen:
Eine Lichtsekunde (ls) ist ca. 300.000 km lang.
Wieviel lang in km ist dann die Strecke von 0,11169 ls?

Tipp: Es ist das gleiche wie hier:
Der Preis für eine Pizza ist 12€.
Was ist der Preis in € für 0,5 Pizzen, das ist eine halbe Pizza?

Frag' doch mal das Kind oder Enkel deines Vertrauens nach etwas Nachhilfe in Mathe. Schulpflicht gibt's doch bei euch auch? Ein bisschen Mathe kann man immer brauchen. Man lernt auch in deinem Alter nie aus.
 

Vielen Dank, relham
Deinen Beitrag konnte ich leider nicht in meinem Beitrag zitieren, das geht scheinbar bei mir nicht. Wenn ich deinen Beitrag zitiere und etwas darunterschreibe, ist das daruntergeschriebene ebenfalls im zitierten enthalten. Und das verwirrt.

Um eine Tabelle zu erstellen, benötige ich noch 2 Angaben:
Auto 1 hat ein Radargerät an seinem Auto fix montiert und messt die Geschwindigkeit von Auto 2 
Auto 8 hat auch Radargerät an seinem Auto fix montiert und messt die Geschwindigkeit von Auto 9
Was messen beide für eine Geschwindigkeit?
Wie schnell ist Auto 2 relativ zu Auto 1 ? Welche Geschwindigkeit zeigt das Radargerät an?
Wie schnell ist Auto 9 relativ zu Auto 8 ? Welche Geschwindigkeit zeigt das Radargerät an?

 

badhofer schrieb:

Wenn ich deinen Beitrag zitiere und etwas darunterschreibe, ist das daruntergeschriebene ebenfalls im zitierten enthalten.

Bevor du etwas "drunterschreibst", musst du auf den roten Pfeil clicken, der erscheint, wenn Du im Editor mit dem Cursor an das Ende des Posts gehst.

badhofer schrieb:

Um eine Tabelle zu erstellen, benötige ich noch 2 Angaben:
 

Die relativistische Addition lautet
w = (u+v)/(1+u·v)
wir haben u und w gegeben, Du suchst v.
v = (w-u)/(1-u·w)
das ist die gleiche Formel wie die relativistische Subtraktion aus Sicht des zweiten dabei beteiligten Autos.
für w(2)-u(1) ergibt sich
0.11380436721696034
und für w(9)-u( ergibt sich
0.9832754588618808

badhofer schrieb:

wie viele Meter

Gefällt Dir das in Metern wirklich besser als in ls?

Ich erweitere mal die Variante 2) um eine Zeitachse senkrecht zur Fahrtrichtung und auch senkrecht zur Startlinie in die Bildschirmebene hinein. Der Anschaulichkeit halber als weitere Raumachse gedacht (Zukunft), in die sich alle Beteiligten mit Lichtgeschwindigkeit bewegen (solange sie keine Geschwindigkeit im 3D-Raum haben).

Wenn ein Auto in Fahrtrichtung Geschwindigkeit aufnimmt, dann muss es in Richtung Zukunft langsamer als Lichtgeschwindigkeit werden, weil es sonst per Vektoraddition Überlichtgeschwindigkeit hätte. Da es sich um eine rechtwinklige Vektoraddition handelt, verhalten sich die Geschwindigkeiten und Strecken in Fahrtrichtung und Zukunft wie Sinus und Cosinus zueinander.

Trägt man die Strecken in Fahrtrichtung und Zukunft in ein Diagramm ein, ergibt sich ein Viertelkreis.

Die Strecke in Richtung Zukunft kann man dann wieder in Sekunden (aus Sicht eines Beobachters ohne Geschwindigkeit im 3D-Raum) zurückrechnen.
Betrachtet man nur die Geschwindigkeiten und Strecken in Fahrtrichtung, bleibt es bei einem linearen Zusammenhang.

Für die Variante aus Sicht des jeweiligen Autofahrers wäre zu klären, ob die sich als ruhend betrachten. Eigentlich sollte denen bewusst sein, dass sie relativistisch unterwegs sind und das sollten die dann auch berücksichtigen.

Rainer Raisch schrieb:

Die relativistische Addition lautet
w = (u+v)/(1+u·v)
wir haben u und w gegeben, Du suchst v.
v = (w-u)/(1-u·w)
das ist die gleiche Formel wie die relativistische Subtraktion aus Sicht des zweiten dabei beteiligten Autos.
für w(2)-u(1) ergibt sich
0.11380436721696034
und für w(9)-u( ergibt sich
0.9832754588618808

Dass die beiden Radargeräte verschiedene Geschwindigkeiten anzeigen, widerspricht dem Relativitätsprinzip. Eine Bewegung kann sich nur auf einen Bezugspunkt beziehen. Die Radargeräte messen nicht, wie schnell sie sich relativ zur Straße bewegen, sondern sie messen lediglich, wie schnell sich das andere Auto relativ zu ihnen bewegt. Das heißt, beide Radargeräte erkennen überhaupt nicht, dass sie sich bewegen. Aufgrund dessen fängt bei beiden Radargeräten der Lorenzfaktor ganz unten an. Der Lorenzfaktor wirkt sich bei beiden gleich aus, weil er sich bei beiden im gleichen Segment bewegt und deshalb messen sie auch gleiche relativistische Geschwindigkeiten.
 

badhofer schrieb:

Rainer Raisch schrieb:

für w(2)-u(1) ergibt sich
0.11380436721696034
und für w(9)-u( ergibt sich
0.9832754588618808

Dass die beiden Radargeräte verschiedene Geschwindigkeiten anzeigen
 

So ist es ja nicht.

Auto 1 hat ein Radargerät an seinem Auto fix montiert und messt die Geschwindigkeit von Auto 2 
Auto 8 hat auch Radargerät an seinem Auto fix montiert und messt die Geschwindigkeit von Auto 9

Rainers Ergebnisse stimmen anscheinend, hab's nachgerechnet.
Dann ist es so:

Auto 1 misst für Auto 2 eine Relativgeschwindigkeit von 0.11380436721696034 c relativ zu sich sich selber, und umgekehrt misst Auto 2 für Auto 1 die gleiche Relativgeschwindigkeit.

Auto 8 misst für Auto 9 eine Relativgeschwindigkeit von 0.9832754588618808 c relativ zu sich sich selber, und umgekehrt misst Auto 9 für Auto 8 die gleiche Relativgeschwindigkeit zu sich selber.

Steinzeit-Astronom schrieb:

Auto 1 misst für Auto 2 eine Relativgeschwindigkeit von 0.11380436721696034 c relativ zu sich sich selber, und umgekehrt misst Auto 2 für Auto 1 die gleiche Relativgeschwindigkeit.

Auto 8 misst für Auto 9 eine Relativgeschwindigkeit von 0.9832754588618808 c relativ zu sich sich selber, und umgekehrt misst Auto 9 für Auto 8 die gleiche Relativgeschwindigkeit zu sich selber.

Das kann nicht sein, dass Auto 1 eine andere Geschwindigkeit von Auto 2 misst als Auto 8 von Auto 9. Beide, sowohl Auto 1 als auch Auto 8 müssen die gleiche Geschwindigkeit messen, denn weder Auto 1 noch Auto 8 erkennen, dass sie sich selber bewegen. Sie messen so, wie wenn sie in Ruhe wären und damit bewegt sich die Messung im selben Segment des Lorenzfaktors, also im ganz niedrigen.

Vor vielen Jahren haben wir so etwas schon mal gehabt in diesem Forum. Das ging ungefähr so, soweit ich mich erinnern kann.

Variante 1)
Ich sitze in einem Zug, der im Bahnhof steht und habe ein ferngesteuertes Auto, von dem ich weiß, dass es 20 km/h fährt. Ich lasse das Auto im Zug fahren und messe mit dem Radargerät in meiner Hand die Geschwindigkeit des Autos. 20 km/h. Eh klar.
Variante 2)
Der Zug bewegt sich mit relativistischer Geschwindigkeit durch den Bahnhof. Wenn mein Radargerät jetzt eine andere Geschwindigkeit des Autos messen würde, dann würde ich erkennen, dass ich mich bewege. Und das kann nicht sein. Ohne nach draußen zu schauen, kann ich in beiden Fällen mit nichts auf der Welt erkennen, ob der Zug sich bewegt oder ruht. 

badhofer schrieb:

Das kann nicht sein, dass Auto 1 eine andere Geschwindigkeit von Auto 2 misst als Auto 8 von Auto 9. [...] denn weder Auto 1 noch Auto 8 erkennen, dass sie sich selber bewegen.

Natürlich erkennen sie das nicht. Wie denn? Sie messen ja nur die Geschwindigkeit des anderen Autos zu sich selber, sonst nichts.

Auto 1 und 2 wissen nichts von Auto 8 und 9 und sie wissen auch nicht, dass die anderen beiden aus Sicht der Straße den gleichen Geschwindigkeitsunterschied haben. Sie wissen nicht mal etwas von der Existenz der Straße. Denn sonst wüssten sie ja, dass sie sich bewegen, wenigstens relativ zur Straße. All das bleibt ihnen aber verborgen.

Gemäß SRT ist die Sache klar:

Die relativistische Addition lautet
w = (u+v)/(1+u·v)

Ein Baum an der Straße ist bewegt zu Auto 2 mit u = -0,222 c (minus = nach hinten vom Auto weg).
Auto1 ist bewegt zum Baum mit v = +0,111 c (plus = nach vorne vom Baum weg).
Auto 1 ist bewegt zu Auto 2 mit w = (u+v) / (1+u·v)
Mit  c = 1 ergibt sich:
w = (-0,222 + 0,111) / (1 + (-0,222 * 0,111)) 
= -0,111 c / (1 + (-0,024642)) 
=  -0,111 c / 0,975358 ≈ -0,114 c (minus = nach hinten von Auto 2 weg).
=> Auto 2 ist bewegt zu Auto 1 mit +0,114 c (plus = nach vorne von Auto 1 weg).

Ein Baum an der Straße ist bewegt zu Auto 9 mit u = -0,999 c (minus = nach hinten vom Auto weg).
Auto 8 ist bewegt zum Baum mit v = +0,888 c (plus = nach vorne vom Baum weg).
Mit  c = 1 ergibt sich:
Auto 8 ist bewegt zu Auto 9 mit w = (u+v) / (1+u·v)
= (-0,999 + 0,888) / (1 + (-0,999 * 0,888)) 
= -0,111 / (1 + (-0,887112)) 
=  -0,111 / 0,112888 ≈ -0,9833 c (minus = nach hinten von Auto 9 weg).
=> Auto 9 ist bewegt zu Auto 8 mit +0,9833 c (plus = nach vorne von Auto 8 weg).

Die Vorzeichen Plus und Minus geben die Richtung der Bewegung an: Plus = nach vorne und Minus = nach hinten. Die Autos 2 bzw. 9 sehen also die Autos 1 bzw. 8 (auch den Baum an der Straße) nach hinten wegfahren. Der Baum sieht die Autos 1 bzw. 8 nach vorne wegfahren.
 

@Steinzeit-Astronom: Wenn die beiden Radargeräte auf der Startlinie stehen, dann ist das alles richtig, was du da schreibst.
Ein Radar messt die Geschwindigkeit von Auto 1, dann die Geschwindigkeit von Auto 2, zieht dann Auto 1 von Auto 2 ab, dann ergibt sich die Geschwindigkeit der beiden Autos relativ zueinander aus der Sicht der Straße. Aufgrund dessen, dass man sich beim Lorentzfaktor im seichten Bereich befindet, ist der Geschwindigkeitsunterschied der beiden Autos nicht so groß.
Das zweite Radar messt die Geschwindigkeit von Auto 8, dann von Auto 9, zieht das Auto 8 von 9 ab, denn ergibt sich die Geschwindigkeit der beiden Autos relativ zueinander aus der Sicht der Straße. Aufgrund dessen, dass man sich beim Lorentzfaktor im extrem hohen Bereich befindet, ist der Geschwindigkeitsunterschied der beiden Autos extrem groß.
Alles richtig so.

Aber beide Radargeräte befinden sich nicht auf der Startlinie, sondern eines im Auto 1 und messt die Geschwindigkeit von Auto 2. Das andere befindet sich in Auto 8 und messt die Geschwindigkeit von Auto 9. Die Sichtweise von der Straße aus spielt da keine Rolle. Beide Radargeräte wissen nicht, dass sie sich bewegen (Relativitätsprinzip). Aufgrund dessen befindet sich die Messung beider Radargeräte im seichten und gleichen Bereich des Lorentsfaktors, nämlich im Bereich von 0 - 0,111 c und messen deshalb auch die gleiche Geschwindigkeit.

 

badhofer schrieb:

Dass die beiden Radargeräte verschiedene Geschwindigkeiten anzeigen, widerspricht dem Relativitätsprinzip. Eine Bewegung kann sich nur auf einen Bezugspunkt beziehen. Die Radargeräte messen nicht, wie schnell sie sich relativ zur Straße bewegen, sondern sie messen lediglich, wie schnell sich das andere Auto relativ zu ihnen bewegt. Das heißt, beide Radargeräte erkennen überhaupt nicht, dass sie sich bewegen. Aufgrund dessen fängt bei beiden Radargeräten der Lorenzfaktor ganz unten an. Der Lorenzfaktor wirkt sich bei beiden gleich aus, weil er sich bei beiden im gleichen Segment bewegt und deshalb messen sie auch gleiche relativistische Geschwindigkeiten.
 

Ich hab mal rot markiert, was falsch ist, und grün, was richtig ist. Der Rest ist ohne Inhalt bzw ohne Sinn bzw ohne Logik.

Sie messen die Relativgeschwindigkeit zu sich selbst, und da diese für beide Messvorgänge unterschiedlich ist, messen sie auch nicht dasselbe.

Vielleicht verstehst du es besser, wenn Du Dich daran erinnerst, dass in Deinem Beispiel alle Autos die Lichtgeschwindigkeit der Lichtstrahlen, die ihnen entgegenkommen und die ihnen hinterhereilen mit c messen.

badhofer schrieb:

Variante 1)
Ich sitze in einem Zug, der im Bahnhof steht und habe ein ferngesteuertes Auto, von dem ich weiß, dass es 20 km/h fährt. Ich lasse das Auto im Zug fahren und messe mit dem Radargerät in meiner Hand die Geschwindigkeit des Autos. 20 km/h. Eh klar.
Variante 2)
Der Zug bewegt sich mit relativistischer Geschwindigkeit durch den Bahnhof. Wenn mein Radargerät jetzt eine andere Geschwindigkeit des Autos messen würde, dann würde ich erkennen, dass ich mich bewege. Und das kann nicht sein. Ohne nach draußen zu schauen, kann ich in beiden Fällen mit nichts auf der Welt erkennen, ob der Zug sich bewegt oder ruh

Das ist zwar richtig, hat mit unserem Rechenexempel allerdings nicht da Geringste zu tun.

Vielleicht verstehst Du es besser, wenn Du Dir Folgendes vorstellst:
Auto 1 fährt mit 0,111 c und es hat ein Spielzeugauto dabei, das es ebenfalls mit 0,111 c davonfahren lässt. Dieses hat ebenfalls ein kleines Modul dabei, das es mit 0,111 c davonschießen kann, usw. Es ist offensichtlich, dass auch nach 1000 derartigen Matroschkapuppen niemals eines dieser Objekte jemals die Lichtgeschwindigkeit v<c gegenüber der Straße erreichen wird, obwohl zwischen je benachbarten Zweien immer die Relativgeschwindigkeit v=0,111 c beträgt.
 

badhofer schrieb:

Das zweite Radar messt die Geschwindigkeit von Auto 8, dann von Auto 9, zieht das Auto 8 von 9 ab, denn ergibt sich die Geschwindigkeit der beiden Autos relativ zueinander aus der Sicht der Straße. Aufgrund dessen, dass man sich beim Lorentzfaktor im extrem hohen Bereich befindet, ist der Geschwindigkeitsunterschied der beiden Autos extrem groß.
 

Nein. Den Geschwindigkeitsunterschied aus Sicht der Straße hast du doch selber auf genau 0,999 c - 0,888 c = 0,111 c festgelegt und hier auch korrekt beschrieben, wie man ihn ausrechnen kann (im Zitat grün markiert).

Der Unterschied aus Sicht der Straße (gemessen mit einem Gerät an der Straße) ist gemäß Vorgabe also immer gleich zwischen zwei aufeinander folgenden Autos. Er ist nicht extrem groß. Er ist nur groß aus Sicht der beteiligten Autos. Genau das ist ja berechnet worden:

Auto 9 fährt dem Auto 8 mit 0,9833 c davon, gemessen mit dem Gerät, das in Auto 8 ruht.
Auto 2 fährt dem Auto 1 mit 0,114 c davon, gemessen mit dem Gerät, das in Auto 1 ruht.
 

badhofer schrieb:

Dass die beiden Radargeräte verschiedene Geschwindigkeiten anzeigen, widerspricht dem Relativitätsprinzip

Das genaue Gegenteil, ist der Fall.
Was Du meinst, wäre eine absolute Geschwindigkeit. So ist es aber nicht. Nur die beiden beteiligten Objekte (A und sind sich über ihre Relativgeschwindigkeit einig. JEDER andere Beobachter (C) misst eine andere Relativgeschwindigkeit zwischen zwei anderen Objekten (A und .

de.wikipedia.org/wiki/Relativistisches_A...Cr_Geschwindigkeiten
Die Konturlinien zeigen die resultierende Geschwindig­keit u x in Schritten von 0,1 c bis 0,9 c, dann 0,95 c, 0,98 c und 0,99 c. Je größer die beiden Ausgangs­geschwindig­keiten, desto stärker weicht das Ergebnis von der arithmetischen Addition ab

Moment, vielleicht verwechsle ich da was.
Angenommen, auf der Straße stehen 2 Autos hintereinander. Auf Auto 1 befindet sich ein Radar, welches dann die Geschwindigkeit von Auto 2 messt. Auch auf der Straße befindet sich ein Radar fix montiert.

Variante 1)
Auto 1 steht relativ zur Straße still, Auto 2 bewegt sich relativ zur Straße mit 0,888 c nach rechts.
Variante 2)
Auto 1 bewegt sich relativ zur Straße mit 0,444 nach links, Auto 2 bewegt sich mit 0,444 c relativ zur Straße nach rechts

Was messen beide Radar in beiden Varianten?

badhofer schrieb:

Was messen beide Radar in beiden Varianten?

Das ortsfeste Radar misst natürlich die von Dir angegebenen Geschwindigkeiten, ebenso das stehende Auto.
Die Radaranzeige im Auto zeigt natürlich im zweiten Fall nicht 0,888 c, sondern die relativistische Addition
w = 0,888c/(1+0,444²) = 0.74177 c

Rainer Raisch schrieb:

Das ortsfeste Radar misst natürlich die von Dir angegebenen Geschwindigkeiten, ebenso das stehende Auto.
Die Radaranzeige im Auto zeigt natürlich im zweiten Fall nicht 0,888 c, sondern die relativistische Addition
w = 0,888c/(1+0,444²) = 0.74177 c

Hallo Rainer
Ich glaube, jetzt wird mir klar, was mir seit Jahrzehnten, seit ich das erste mal von der SRT gehört habe, nicht klar geworden ist.
Kannst du mir noch die beiden 0.xxxxx c errechnen. 

Variante 1)
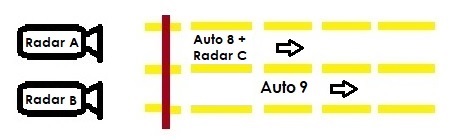
Radar A messt, dass sich Auto 1 mit 0,111 c relativ zu ihm entfernt
Radar B messt, dass sich Auto 2 mit 0,222 c relativ zu ihm entfernt
Radar C messt, dass sich Auto 2 mit 0.xxxxx c relativ zu ihm entfernt




Variante 2)
Radar A messt, dass sich Auto 8 mit 0,888 c relativ zu ihm entfernt
Radar B messt, dass sich Auto 9 mit 0,999 c relativ zu ihm entfernt
Radar C messt, dass sich Auto 9 mit 0.xxxxx c relativ zu ihm entfernt

badhofer schrieb:

Kannst du mir noch die beiden 0.xxxxx c errechnen.

Hatten wir das nicht schon in  # 624 / 625 ?
A und B sind ja dasselbe IS. Der Punkt ist, dass auch die Messungen von A und C im selben IS von C korrekt sind, weil die Messung A ja in diesen beiden IS gleich ist. Genauso wie B und C dasselbe IS repräsentieren, weil diese beiden Messungen ja auch für das zweite Auto richtig wären. Nur können halt nicht alle drei Messungen in einem IS richtig sein. Die relativistische Addition bzw Subtraktion geht aber deshalb für jede der drei Messungen. A (+) C = B
C = B (-) A = B (+) -A
(0,222-0,111)/(1-0,111*0,222) = 0,1138
(0,999-0,888)/(1-0,888*0,999) = 0,983